§13 関数の微分 I

今回からいよいよ関数の微分に進んでいきたいと思います。と言っても、微分とはある関数の極限値で定義されるものなので、これまで扱ってきた関数の極限 (あるいは数列の極限) を使えば特別新たな概念が登場するというわけでもありません。しかしながら、関数の微分を導入すると、関数の持つ性質をより詳しく調べる事が出来るようになり、また物理学やファイナンスその他多くの分野への応用の幅も大きく広がります。

微分の定義

$I\subset \mathbb {R}$ 上で定義された実数値関数 $f$ を考えます。説明の都合上、当面の間は $I$ は開区間であると考えて下さい。この時、点 $x_0\in I$ における関数 $f$ の微分について以下の定義を与えます。

まず最初の注意として、$x_0$ を固定した時に以下で定義される関数 $$h(x) = \frac{f(x) - f(x_0)}{x - x_0}$$ は $x_0$ において定義されていません。§1 でも一言触れましたが、(1) が考えているのは $h(x)$ の「$x\rightarrow x_0$ とした時の極限」であって、$h(x_0)$ の値自身は関係ないどころか (定義されていないので) 考える事が出来ません。そのため、もし (1) の極限値が $f'(x_0)$ である事をイプシロン・デルタ論法で書くならば、 $$\begin{align*} &^\forall \varepsilon > 0, \ \ ^\exists \delta > 0\ \ \mbox {s.t.}\\ &\hspace{10mm}0 < |x - x_0| < \delta \ \Longrightarrow \ |h(x) - f'(x_0)| < \varepsilon \end{align*}$$ あるいは $$\begin{align*} &^\forall \varepsilon > 0, \ \ ^\exists \delta > 0\ \ \mbox {s.t.}\\ &\hspace{10mm}^\forall x\in I\setminus \{x_0\}, \ |x - x_0| < \delta \ \Longrightarrow \ |h(x) - f'(x_0)| < \varepsilon \end{align*}$$ のように $x\neq x_0$ である点について注意しておかなければなりません¹。

次に、上で定義される $h(x)$ は、$xy$-平面上で考えるならば以下の 2 点 $$(x_0, f(x_0)), \ \ (x, f(x))$$ を結ぶ直線の傾きに対応しており、この時もし $x$ を $x_0$ に限りなく近付けていけば、その傾き $h(x)$ は「$y = f(x)$ のグラフの $x_0$ における接線の傾き」に近付いていくと考えられます (下図参照)。これが (一階) 微分の直観的なイメージであり、よって「関数を微分する」とは「傾きを調べる」事を意味していると言えます。

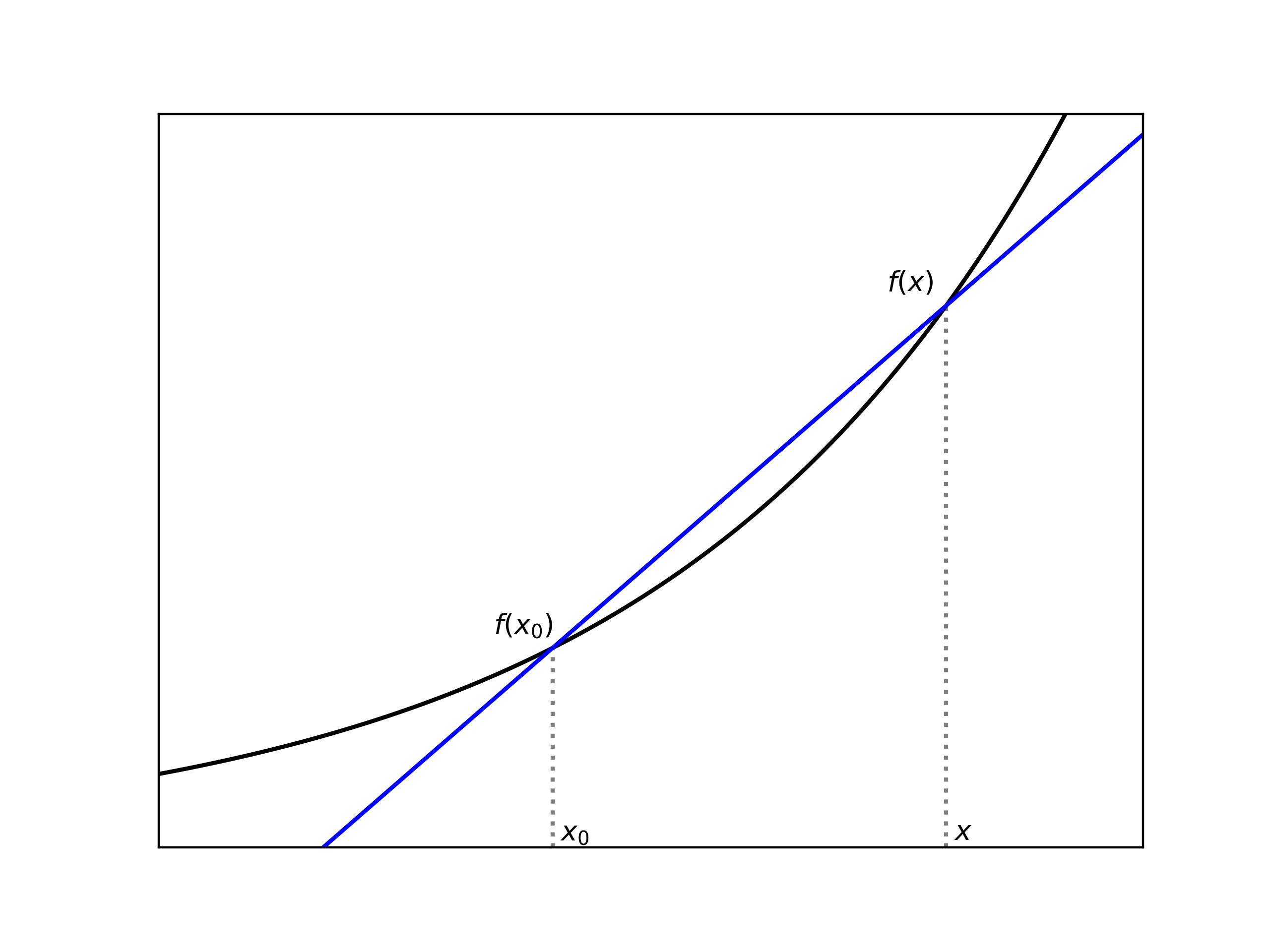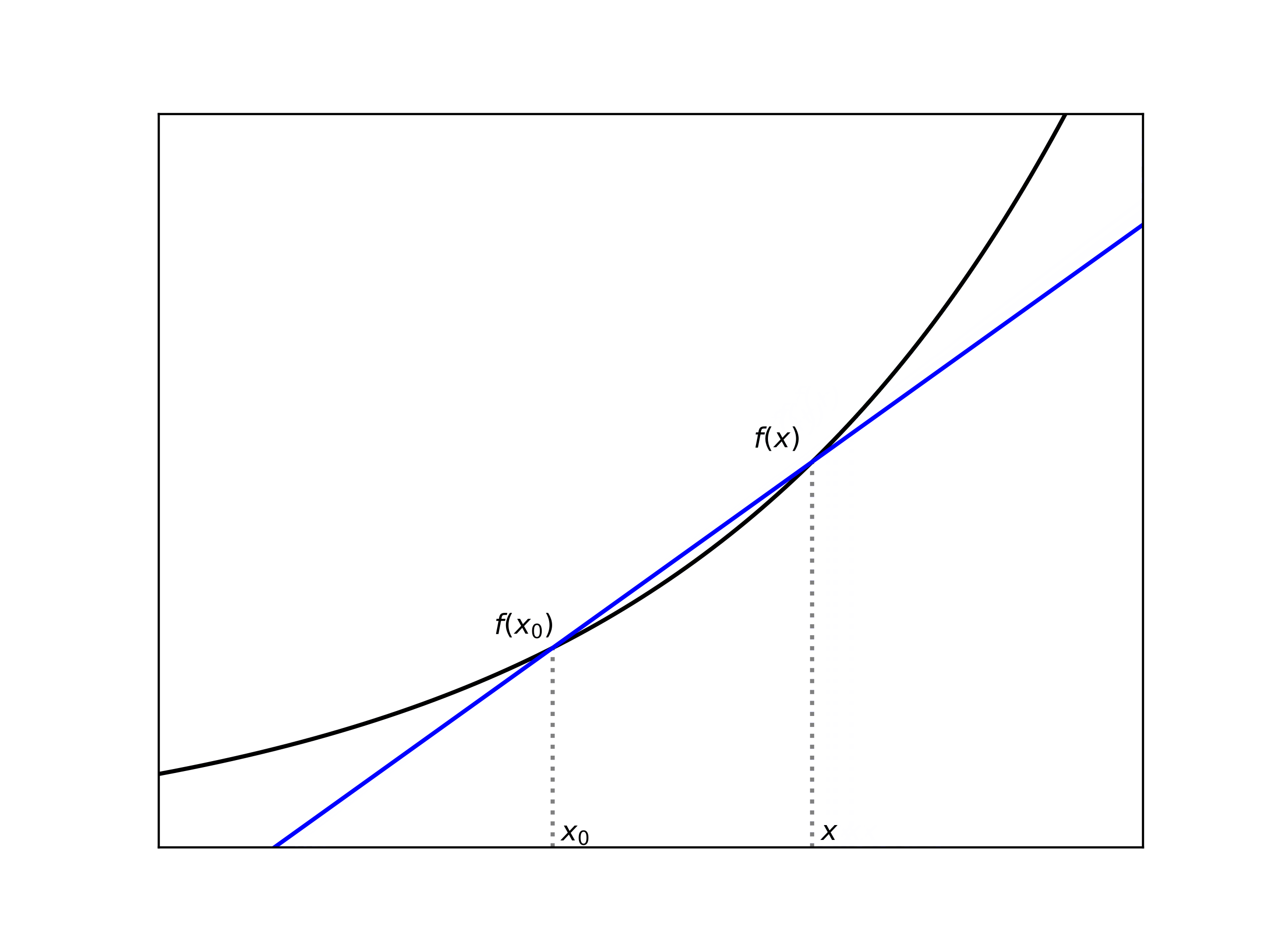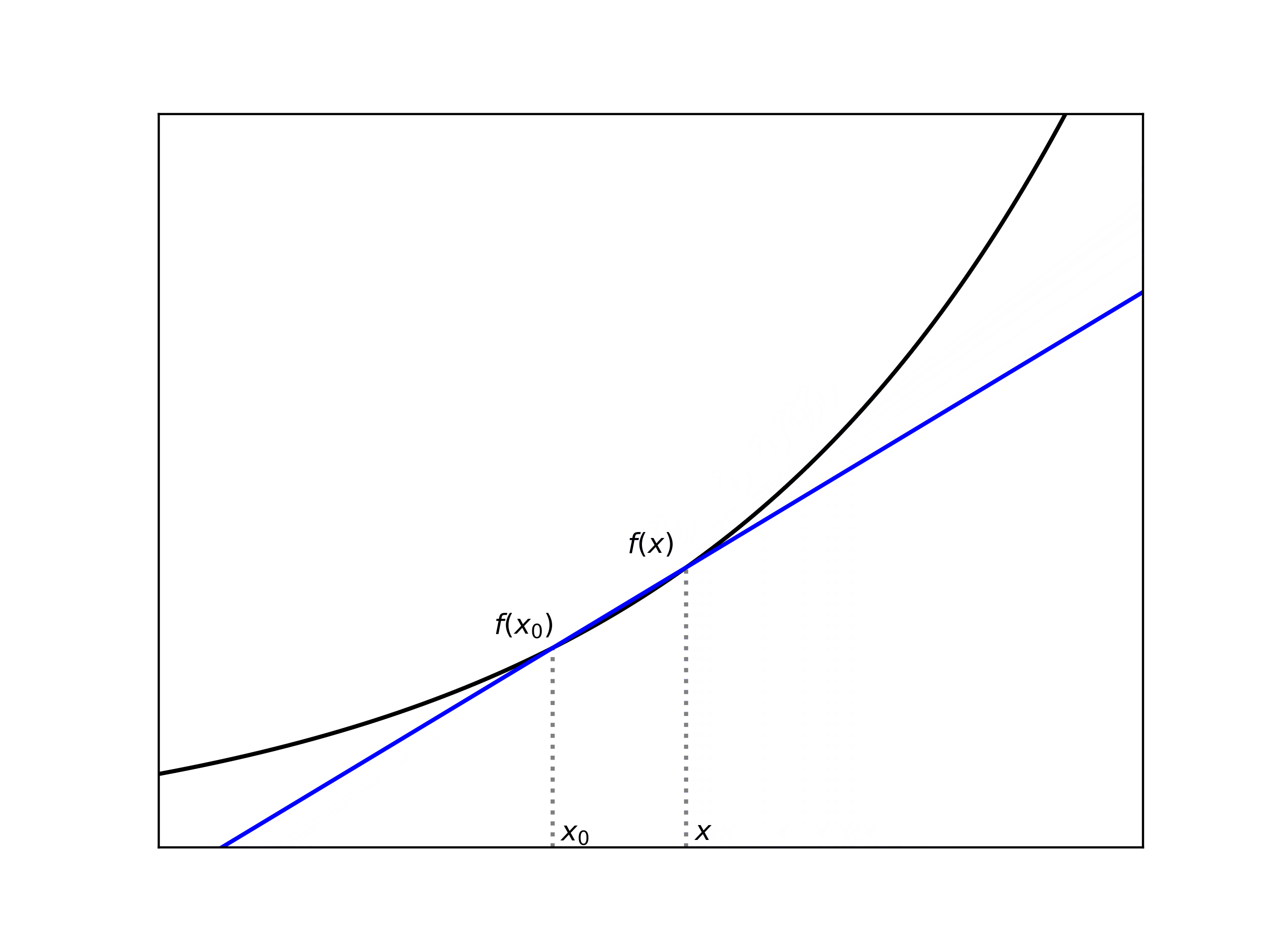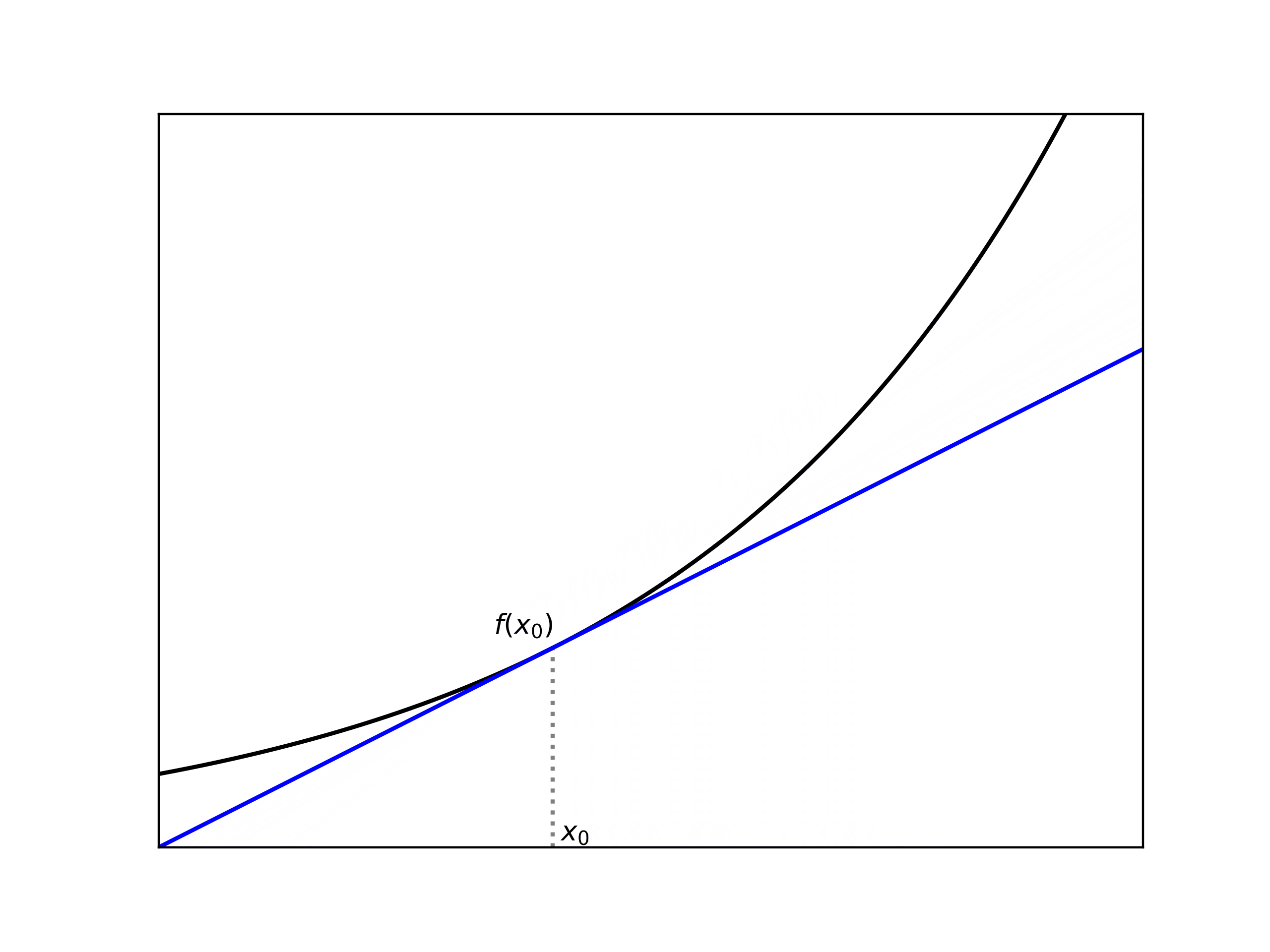
更に、微分可能な関数はその点で連続でもある事に注意しておきます。実際、$f$ が $x_0\in I$ で微分可能であるならば、やはり上の記号 $h(x)$ を使って $$\begin{align*} f(x) - f(x_0) &= h(x)(x - x_0)\\ &\longrightarrow f'(x_0)\cdot 0 = 0, \ \ x\rightarrow x_0 \end{align*}$$ が得られます ($h(x)$, $x - x_0$ が共に $x\rightarrow x_0$ の下で収束しているので、§9 に登場した関数の加減乗除の極限に関する命題が使えます)。

上の定義では $I$ の中の一点 $x_0$ のみの微分可能性を考えましたが、もし $f$ が $I$ 上の全ての点で微分可能であるならば、各点における微分係数 $(f'(x_0))_{x_0\in I}$ を $I$ 上の実数値関数とみなす事が出来そうです。

上と同様、$I$ 上で微分可能な関数は常に $I$ 上で連続となります。しかし連続関数が常に微分可能であるとは限りません。例えば折れ線関数 $$f(x) = \left\{ \begin{align*} x \ & \ (x\geq 0)\\ 0 \ & \ (x\ < 0) \end{align*} \right.$$ は $\mathbb {R}$ で連続ですが原点で微分可能ではありません。実際、もし $f$ が原点で微分可能であるとしたら、§8 の命題 1 より、$0$ に収束するあらゆる数列 $(a_n)_n$ に対して $f(a_n)$ が同じ値に収束しなければなりませんが、$a_n = 1/n$, $b_n = -1/n$ とすると ($f(0) = 0$ に注意して) $$\frac{f(a_n)}{a_n} = 1 \ \longrightarrow 1, \ \ n\rightarrow \infty$$ かつ $$\frac{f(b_n)}{b_n} = 0 \ \longrightarrow 0, \ \ n\rightarrow \infty$$ となってしまい、両者の極限値が一致しません。これは「区間全体で連続だが区間のうち一点で微分不可能」な例ですが、世の中には更に「区間全体で連続だが区間の至るところで微分不可能」な関数が存在する事も知られています。その代表的な例として Weierstrass 関数が知られており、これを正確に図示する事は出来ないのですが概ね下図のように「連続的に繋がっているが至るところでギザギザしている曲線」をグラフに持つ関数となっています。

更には、確率論や数理ファイナンス、金融工学等で頻繁に登場する連続時間確率過程である Brown 運動 (Brownian motion) あるいは Wiener 過程 (Wiener process) もまた、(ほとんど確実に) 「連続だが至るところで微分不可能」な動きをする関数であり、上の Weierstrass 関数のように「どこを見てもギザギザ」な形状をしています (下図参照)³。

これらのように、世の中には変わった関数が多数存在している事、よって「何となく成り立っていそうだ」という命題をきちんと確認 (証明) せず安易に信じてはいけない事には注意しなければならないのですが、しかしこれまで紹介したような基本的な初等関数の多くは (適切な定義域の上で) 微分可能であるので、当面はそこまで神経質にならなくとも問題ありません。

最後にもう一つ、微分に対する定義を与えておきます。

我々はこれまで連続関数に対する一般的な性質を調べてきました。という事は、今後 $C^1$-級関数 $f$ を扱う際に、これまで得られた連続関数に対する定理等を $f$ だけでなく $f'$ にも適用出来る事になります。但し連続関数に関するいくつかの定理は $I$ が有界閉区間であるという仮定が置かれていたのに対して、今我々が考えている定義域 $I$ は開区間となっている点には注意しましょう。

初等関数の微分 I

上で与えた定義に従って、これまで紹介した初等関数の導関数を導いてみましょう。まず冪乗関数 $$f_n: \mathbb {R}\ni x\ \longmapsto \ x^n\in \mathbb {R}$$ を考えてみます。ここで $n$ は「とりあえず」自然数としておきます。実は更に ($0$ 以外の) 一般の実数の場合にも概ね同じ結果が得られるのですが⁴、ここで紹介する証明と同じ方法では結論を得る事が出来ません。さて、任意の $x_0\in \mathbb {R}$ を取ると $$\begin{align*} \frac{f_n(x) - f_n(x_0)}{x - x_0} &= \frac{x^n - x^n_0}{x - x_0}\\ &= \frac{(x - x_0)\sum ^{n-1}_{k=0}x^{n-1-k}x_0^k}{x - x_0}\\ &= \sum ^{n-1}_{k=0}x^{n-1-k}x_0^k\\ &\longrightarrow \ \sum ^{n-1}_{k=0}x^{n-1}_0 = nx_0^{n-1}, \ \ x\rightarrow x_0 \end{align*}$$ となる事から、$f_n$ は $\mathbb {R}$ 上で微分可能であり $f'_n(x) = nx^{n-1}$ である事が分かりました。そして $f'_n$ は $\mathbb {R}$ 上連続である事から $f_n\in C^1(\mathbb {R})$ である事も分かります。

また明らかに定数関数 $f_0: x \mapsto c$ ($c$ は所与の実数) は $\mathbb {R}$ 上 $C^1$-級であり $f'_0(x) = 0$ となります (気になる人は証明を書いてみて下さい)。

関数 $f_{-1}: x\mapsto \frac{1}{x}$ は $x = 0$ において定義されていないので、定義域を $(0, \infty)$ 及び $(-\infty, 0)$ に分けて考えてみると、いずれの場合でも $x_0\neq 0$ として $$\frac{f_{-1}(x) - f_{-1}(x_0)}{x - x_0} = -\frac{1}{xx_0} \longrightarrow -\frac{1}{x^2_0}, \ \ x\rightarrow x_0$$ となり、ここから $f'_{-1}(x) = -1/x^2$ $(x\neq 0)$ であり、$f_{-1}$ は $(0, \infty)$ または $(-\infty, 0)$ の上で $C^1$-級である事が分かります。

次に指数関数 $\exp : \mathbb {R}\ni x \longmapsto e^x\in (0, \infty)$ の微分を考えてみます。ここで、§11 で示した定理 1 が再登場します。 $$e^x \geq 1 + x, \ \ ^\forall x\in \mathbb {R} \tag {2}$$ §11 の定理 1 では $x$ が有理数の場合のみを対象としていましたが、$x$ を任意の実数に拡張しても上の (2) 式は正しい事についても既に触れました。そして §11 と同様の議論によって $$1 + x \leq e^x \leq \frac{1}{1-x}, \ \ x\in ( -1, 1)$$ が得られるのも問題ないかと思います。すると各辺から $1 (= e^0)$ を引いて $x$ で割ってやると $$1 \leq \frac{e^x - e^0}{x - 0} \leq \frac{1}{1-x}, \ \ x\in (-1, 1)\setminus \{0\}$$ が得られ、$x\rightarrow 0$ として挟み撃ちの原理を使うと $$(e^x)'|_{x=0} = \lim _{x\rightarrow 0}\frac{e^x - e^0}{x - 0} = 1$$ となり⁵、まず $\exp$ が原点 $0$ において微分可能である事、そして微分係数が $1$ である事が示されます。次に任意の $x_0\in \mathbb {R}$ に対して、指数法則を使えば $$\frac{e^x - e^{x_0}}{x - x_0} = \frac{e^{x_0}e^{(x - x_0)} - e^{x_0}}{x - x_0} = e^{x_0}\cdot \frac{e^{x - x_0} - 1}{x - x_0}$$ となりますが、 $$\lim _{x\rightarrow x_0}\frac{e^{x - x_0} - 1}{x - x_0} = \lim _{y \rightarrow 0}\frac{e^y - 1}{y} = 1$$ である事は既に見たので、これらを合わせて $$\lim _{x\rightarrow x_0}\frac{e^x - e^{x_0}}{x - x_0} = e^{x_0}$$ が従います。以上から指数関数は $\mathbb {R}$ 上で微分可能であり、その導関数は $e^x$ 自身、即ち $(e^x)' = e^x$ である事が分かりました。指数関数が連続であった事と合わせると $\exp \in C^1(\mathbb {R})$ である事も分かります。

これら以外の初等関数の導関数を同様に計算する事も可能ですが、その前に関数の微分に関する基本的な性質を導いておいて、それらを適用しながら他の初等関数の微分を計算する方が楽なので、他の初等関数の微分はまた後で扱う事にして一般論を進めます。

微分の性質 I

まず、微分に関する最も基本的な性質 (あるいは公式) を見ていきます。

証明. 2. のみ示す (1. は各自)。$x\in I\setminus \{x_0\}$ として $$\begin{align*} &\frac{(fg)(x) - (fg)(x_0)}{x - x_0} = \frac{f(x)g(x) - f(x_0)g(x_0)}{x - x_0}\\ &= \frac{f(x)g(x) - f(x_0)g(x) + f(x_0)g(x) - f(x_0)g(x_0)}{x - x_0}\\ &= \frac{f(x) - f(x_0)}{x - x_0}\cdot g(x) + f(x_0)\cdot \frac{g(x) - g(x_0)}{x - x_0}\\ &\longrightarrow f'(x_0)g(x_0) + f(x_0)g'(x_0), \ \ x \rightarrow x_0 \end{align*}$$ が成立。ここで、$g$ が $x_0$ で微分可能ゆえ連続である事を用いた。

次の定理は合成関数の微分公式あるいは連鎖率 (chain rule) と呼ばれており、具体的な微分計算に留まらず多くの場面で活躍する事になります。

定理自体の証明は丁寧に行わなければなりませんが、直観的には以下のように考えれば分かりやすいと思います。 $$\begin{align*} &\frac{g\circ f(x) - g\circ f(x_0)}{x - x_0}\\ &= \frac{g(f(x)) - g(f(x_0))}{f(x) - f(x_0)}\cdot \frac{f(x) - f(x_0)}{x - x_0}\\ &\longrightarrow g'(f(x_0))f'(x_0), \ \ x\rightarrow x_0　\tag {4} \end{align*}$$ (勿論、$x\neq x_0$ だからといって $f(x) - f(x_0) \neq 0$ とは限らないので、このままでは証明として不十分です。) 更に、$y = f(x)$, $z = g(y)$ と表せば、(3) (において $x_0$ を $x$ に置き換えたもの) は Leibniz の記法を用いれば $$\frac{dz}{dx} = \frac{dz}{dy}\frac{dy}{dx}$$ となり、あたかも $dx, dy$ 等を数と思って普通の分数を計算しているかのように表す事が出来ます。今の場合、$dy$ が (4) における $f(x) - f(x_0)$ に対応しています。

定理 1 の証明. 任意の $\varepsilon > 0$ を取り固定する。$g$ は $f(x_0)$ において微分可能なので、ある $\delta > 0$ が存在して $0 < |y - f(x_0)| < \delta$ なる任意の $y\in J$ に対して $$\left|\frac{g(y) - g(f(x_0))}{y - f(x_0)} - g'(f(x_0))\right| < \varepsilon$$ 即ち $$\left|g(y) - g(f(x_0)) - g'(f(x_0))(y - f(x_0))\right| < \varepsilon |y - f(x_0)|$$ が成立する。一方、$f$ は $x_0$ において微分可能なので、ある $\eta > 0$ が存在して $0 < |x - x_0| < \eta$ なる任意の $x\in I$ に対して $$\left|\frac{f(x) - f(x_0)}{x - x_0} - f'(x_0)\right| < \varepsilon \tag {5}$$ が成り立つ。そこで $$\zeta = \eta \wedge \frac{\delta}{\varepsilon + |f'(x_0)|} \ ( > 0)$$ と定義すれば、$|x - x_0| < \zeta$ なる任意の $x\in I$ に対して $$\begin{align*} |f(x) - f(x_0)| \leq & |f(x) - f(x_0) - f'(x_0)(x - x_0)|\\ &+ |f'(x_0)(x - x_0)|\\ \leq & (\varepsilon + |f'(x_0)|)|x - x_0| < \delta \end{align*}$$ となる。

以上の事から、$0 < |x - x_0| < \zeta$ の時に $$\begin{align*} &\left| \frac{g\circ f(x) - g\circ f(x_0)}{x - x_0} - g'(f(x_0))f'(x_0)\right|\\ \leq & \left| \frac{g\circ f(x) - g\circ f(x_0) - g'(f(x_0))(f(x) - f(x_0))}{x - x_0}\right|\\ &+ |g'(f(x_0))|\cdot \left| \frac{f(x) - f(x_0)}{x - x_0} - f'(x_0)\right|\\ \leq & \varepsilon \cdot \left|\frac{f(x) - f(x_0)}{x - x_0}\right| + |g'(f(x_0))|\varepsilon \leq \ ^\exists M\varepsilon \end{align*}$$ が得られる⁶。よって題意は示された。

定理 1 は二つの関数の合成に対する微分を与えていますが、数学的帰納法を用いれば、任意の $n\in \mathbb {N}$ 個の関数の合成に対する微分を計算する事も出来ます。例えば $$(f_1\circ f_2\circ f_3\circ f_4)'(x) = f'_1(f_2\circ f_3 \circ f_4(x))f'_2(f_3\circ f_4(x))f'_3(f_4(x))f'_4(x)$$ といった具合です。また定理 1 と公式 $(1/x)' = -1/x^2$ 及び命題 1 の 2. を組み合わせれば商の微分公式 $$\begin{align*} \left(\frac{1}{f(x)}\right)' &= -\frac{f'(x)}{f(x)^2}\\ \left(\frac{g(x)}{f(x)}\right)' &= \frac{f(x)g'(x) - f'(x)g(x)}{f(x)^2} \tag {6} \end{align*}$$ を得る事が出来ます (詳細は省略します)。

次に、逆関数の微分を考えます。

(7) において $y_0 = f(x_0)$ とおくと $$(f^{-1})(y_0) = \frac{1}{f'(f^{-1}(y_0))}$$ となります。即ち、ある点 $y_0$ における逆関数の微分を求めたければ、元の関数の $f^{-1}(y_0)$ における微分係数を求めてその逆数を取れば良い、という事です。今の場合もやはり Leibniz の記法を用いると直観的に分かりやすく、$y = f(x)$ とする時 $x = f^{-1}(y)$ という関係が成り立つ事に注意して $$\frac{dx}{dy} = \frac{1}{\frac{dy}{dx}}$$ となり、左辺の分子分母を形式的に $dx$ で割ったものが (7) (において $x_0 = x$ としたもの) に対応しています。

定理 2 の証明. $y_0 = f(x_0)$ と置き、$(y_n)_n$ を $y_0$ に収束する数列で $^\forall n: y_n\neq y_0$ なるものとする。この時 $x_n = f^{-1}(y_n)$ と置くと、$f^{-1}$ の単射性から $^\forall n: x_n \neq x_0$ であり、また $f^{-1}$ の $y_0$ における連続性から $x_n\rightarrow x_0$, $n\rightarrow \infty$ である⁸。よって $$\begin{align*} \frac{f^{-1}(y_n) - f^{-1}(y_0)}{y_n - y_0} &= \left(\frac{f(x_n) - f(x_0)}{x_n - x_0}\right)^{-1}\\ &\longrightarrow \frac{1}{f'(x_0)}, \ \ n\rightarrow \infty \end{align*}$$ が得られる。$(y_n)_n$ の取り方は任意であったため、 $$\lim _{y\rightarrow y_0}\frac{f^{-1}(y) - f^{-1}(y_0)}{y - y_0} = \frac{1}{f'(x_0)}$$ が示された。

初等関数の微分 II

上で示した命題や定理を使えば、今まで紹介してきた初等関数の大半の微分を計算する事が出来るようになります。

まず多項式関数の微分が $$\begin{align*} &(a_nx^n + a_{n-1}x^{n-1} + \cdots + a_1x + a_0)'\\ &= na_nx^{n-1} + (n-1)a_{n-2}x^{n-2} + \cdots + a_1, \ \ x\in \mathbb {R} \end{align*}$$ となる事は命題 1 の 1. から明らかでしょう。なお、上では $x^n$ の導関数を直接計算によって導きましたが、$x' = 1$ さえ示してしまえば後は命題 1 の 2. と数学的帰納法から任意の $n\in \mathbb {N}$ について $(x^n)' = nx^{n-1}$ である事を容易に示す事が出来ます。同様に、$1/x$ の微分と命題 1 の 2. を組み合わせれば、実は $n$ が負の整数である場合にも $(x^n)' = nx^{n-1}$ となっている事を確認出来ます (但し $x\neq 0$ としなければならない点に注意)。

次に対数関数の微分ですが、定理 2 を使えば $$(\log x)' = (\exp ^{-1}x)' = \frac{1}{\exp (\log x)} = \frac{1}{x}, \ \ x > 0$$ が直ちに従います⁹。またここから所与の $a > 0$ に対して $$(a^x)' = (e^{x\log a})' = e^{x\log a}\cdot (x\log a)' = a^x\log a, \ \ x\in \mathbb {R}$$ となる事が分かりますし、同様に所与の $\alpha \in \mathbb {R}$ に対して $$(x^\alpha)' = (e^{\alpha \log x})' = e^{\alpha \log x}\cdot (\alpha \log x)' = \alpha \cdot \frac{x^\alpha}{x} = \alpha x^{\alpha - 1}, \ \ x > 0$$ も得られます。

双曲線関数の微分計算も定理 2 の良い練習になるかもしれません。まず $$(\sinh x)' = \cosh x, \ \ (\cosh x)' = \sinh x$$ となる事は指数関数の微分と命題 1 の 1. から明らかでしょう。また (6) から $$\begin{align*} &(\tanh x)' = \left( \frac{e^{2x} - 1}{e^{2x} + 1}\right)'\\ &= \frac{2e^{2x}\cdot (e^{2x} + 1) - (e^{2x} - 1)\cdot 2e^{2x}}{(e^{2x} + 1)^2}\\ &= \frac{4e^{2x}}{(e^{2x} + 1)^2} = \frac{4}{(e^x + e^{-x})^2} = \frac{1}{\cosh ^2x} \end{align*}$$ が得られますが、更に $\cosh ^2x - \sinh ^2x = 1$ と合わせると $$(\tanh x)' = 1 - \tanh ^2x$$ とも表せる事が分かります。

上と定理 2 を組み合わせれば逆双曲線関数 (双曲線関数の逆関数) 達の微分も計算出来ます。例えば $$(\tanh ^{-1}x)' = \frac{1}{1 - \tanh ^2(\tanh ^{-1}x)} = \frac{1}{1 - x^2}$$ です。なお $\tanh ^{-1}x$ は対数関数を用いて表現する事も出来ていたので、それを使って直接 $$\begin{align*} (\tanh ^{-1}x)' &= \left(\frac{1}{2}(\log (1+x) - \log (1-x))\right)'\\ &= \frac{1}{2}\left( \frac{1}{1+x} + \frac{1}{1-x}\right) = \frac{1}{1-x^2} \end{align*}$$ と計算する事も可能です。他の逆双曲線関数に関しては結果のみ掲載します。 $$(\sinh ^{-1}x)' = \frac{1}{\sqrt{x^2 + 1}}, \ \ (\cosh ^{-1}x)' = \frac{1}{\sqrt{x^2 - 1}}$$ それぞれ定義域は異なりますが、いずれも適当な定義域の上で $C^1$-級になっています。

ここまでのまとめ

今回、ついに関数の微分を導入するに至りました。微分の定義は関数の極限の概念を用いて直接表現する事が出来ましたが、これから扱う積分 (Riemann 積分) の定義はやや厄介であり、§1 や §12 に登場した区分求積法のような方法をより精密に行う必要があります。しかし実はこの「微分」と「積分」という異なる概念が互いの逆演算の形で関係しあっている事が分かり、微分積分学の基本定理 (fundamental theorem of calculus) として知られるようになりました。

本講座では微分に関する更なる性質を調べる前にまず積分の定義を与え、微分積分学の基本定理を得るまでの最短コースを進んでみます。そして基本定理を武器として微分や積分に関する様々な性質を示していきたいと思います¹⁰。

今回紹介した連鎖律は、近年注目を集めている機械学習、特に (人工) ニューラルネットワークにおける誤差逆伝播法 (backpropagation) における要と言えます¹¹。何故この手法がニューラルネットワークの実装において有効なのか、連鎖律がどのように活用されているのかについて、番外編として「一次元の最も単純なニューラルネットワーク (あるいはパーセプトロン)」を取り上げて紹介したいと思います。